Concrete slabs play a vital role in most buildings and structures, providing the necessary support in the withstanding and distribution of loads. Proper designing of concrete slab ensures the safety and functionality of the building. The design of a concrete slab requires precise calculations to meet the safety standards, and longevity. This blog will explore how to design a concrete slab, based on IS code 456:2000.
Basics of Reinforced Concrete Slab Design As per IS 456:2000
Effective Span of Slab
The Effective Span of the Slab shall be the lesser of the two
l = clear span + d (effective depth)
l = Center-to-center distance between the support
Depth of Slab
The depth of the slab depends on bending moment and deflection. The trial depth can be obtained by,
- Effective depth, d = Span/((l/d)Basic × modification factor).
- To obtain the modification factor, the percentage of steel used for the slab can be assumed from 0.2 to 0.5%.
- The effective depth (d) of two-way slabs for a short span is ≤3.5m and the loading class is <3.5 kN/m² (As per cl.24.1, IS 456:2000).
Span to Effective Depth Ratio
| Type of Support | Fe-250 | Fe-415 |
| Simply Supported Slab | l/35 | l/28 |
| Continuous Slab | l/40 | l/32 |
This can also be calculated using the thumb rule,
- One Way Slab, d = (l/22) to (l/28)
- Two Way Simply Supported Slab, d = (l/20) to (l/30)
- Two Way Restrained Slab, d = (l/30) to (l/32)
Load on Slab
The load on the slab comprises— Dead load, floor finish, and live load.
- Dead load = D x Unit weight of concrete (where D is the thickness of the slab in m)
- Floor finish = 1 to 2 kN/m² (Assumption)
- Live load = 3 to 5 kN/m² (Assumption depending on the occupancy of the building)
Detailing Requirements As Per Is 456:2000
Reinforcement (Nominal) Cover
Nominal cover, if the diameter of the bar is not less than 12 mm:
- Mild exposure = 20 mm
- Moderate exposure = 30 mm
If the diameter of the bar is less than 12 mm, the nominal cover will be reduced by 5 mm. Therefore, the nominal cover for main reinforcement will be 15 mm for mild exposure with bars less than 12mm in diameter.
Minimum Reinforcement
The reinforcement in either direction of the slab should not be less than,
- 0.15% of the total cross-sectional area for Fe-250 steel
- 0.12% of the total cross-sectional area for Fe-415 and Fe-500 steel.
Spacing of Bars
The bars should be equally placed and the maximum spacing should not exceed,
- 3d or 300 mm, whichever is less for main steel.
- 5d of 450 mm, whichever is less for distribution steel.
Where, ‘d’ is the effective depth of the slab.
It is important to note that the minimum clear spacing of bars should not be less than 75 mm, preferably 100 mm.
Maximum Diameter of Bar
According to IS 456:2000, the maximum diameter of the bar in the slab should not exceed D/8, where ‘D’ is the slab’s total depth.
Step-by-Step Design Procedure As Per IS 456:2000
Determine the Type of Slab
The first step in the design of a slab is to understand whether the slab is one-way or two-way based on the length of the longer side and the shorter side
- If lx/ly ≥ 2, then it is a one-way slab
- If lx/ly < 2, then it is a two-way slab.
Determine Span-to-Depth Ratio (l/d)
The next step is to assume the depth of the slab to satisfy the deflection control criteria, based on (Clause 23.2.1 of IS Code 456:2000, Page 37)
- For a simply supported slab, the l/d ratio up to 10m is 20.
- For a cantilever slab, the l/d ratio up to 10m is 7.
- For a continuous slab, the l/d ratio up to 10m is 26.
- For spans above 10m, the l/d values should be multiplied by 10/span in metres, except for the cantilever slab, where deflection calculations are made.
Hence, to satisfy the defection criteria, the l/d ratio should be greater than or equal to 25, for the simply supported slab, and greater than or equal to 10 for the cantilever slab.
Calculation of Effective Span
According to Clause 22.2, IS 456:2000, the effective span can be determined by taking the lowest value among the two.
- Clear span + effective depth
- The centre-to-centre distance of support
Calculation of Loads
The self-weight of the load, floor finish, and live loads are calculated.
- Dead Load (DL) = Unit weight of the concrete x Thickness of Slab
- The Live Load can be calculated based on the types of usage of the building, the loads due to movable items and furnishings (as per IS 856, Part 2).
- Total Load / Ultimate Load (Wu) = Dead Load + Live Load
- Factored Load = Total Load x 1.5 (safety factor)
Bending Moment
The bending moments are calculated based on the type of slab, whether it is a simply supported slab or a cantilever slab.
Bending Moment,
- Mu = Wu x l²/8 (for simply supported slab)
- Mu = Mu = Wu x l²/2 (for cantilever slab)
Area of Reinforcement & Check for Depth
The area of the reinforcement can be calculated using the formula,
Mu = 0.87 fy Ast d(1 – (Ast fy)/(bd fck))
Where, Mu is the calculated moment
fck is the strength of the concrete
fy is the strength of the steel
Ast is the area of steel
b is the width of the slab
d is the depth of the slab
Design of Reinforcement
According to Clause 26.5.2.1 of IS 456:2000, the mild steel reinforcement in either direction in slabs shall not be less than 0.15% of the Total Cross Sectional Area. However, this value can be reduced to 0.12%, when HYSD bars are used.
According to Clause 26.5.2.2 of IS 456:2000, the diameter of reinforcing bars should not exceed 1/8th of the total thickness of the slab.
Check for Shear
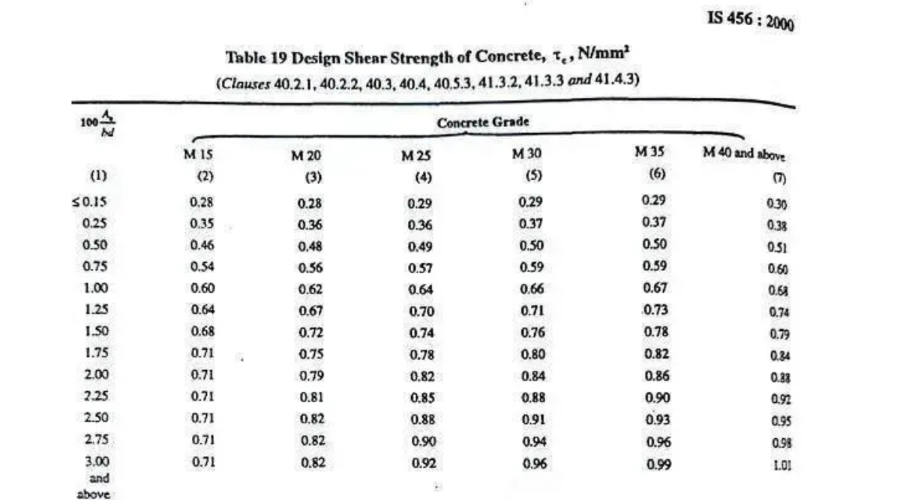
source: CivilConcept
The design shear strength of the concrete can be determined based on the concrete grade and (100 x As/bd), based on Table 19, and the clauses 40.2.1, 40.2.2, 40.3, 40.4, 41.3.2, 41.3.3, and 41.4.3.
Check for Deflection
According to Clause 23.2.2 of IS 456:2000, the final deflection due to all loads including the effects of temperature, creep, and shrinkage and measured from the as-cast level of the supports of floors, roofs and all other horizontal members should not normally exceed span/250.
The defects, including the effects of temperature, creep and shrinkage, occurring after the erection of partitions and the application of finishes should not normally exceed span/350 or 20 mm, whichever is less.
Conclusion
To conclude, designing a concrete slab is of utmost importance to ensure the safety, stability, and longevity of the structure. By considering the factors like load distribution, reinforcement, deflection, and properties, slabs can be built within the codes, to work effectively under various loading conditions, maintaining the structural integrity.

